確固たる数学的知識を身につけ、
他分野への応用にもアプローチ。
1
独自の5専攻融合型カリキュラムと多彩な研究ゼミ
2
日本を代表する企業との連携による実学教育、
最新鋭の設備を導入した環境
最新鋭の設備を導入した環境
3
就職はもちろん国公立大学大学院進学・資格取得を強力サポート
CURRICULUM
授業ピックアップ
理工学実践演習Ⅰ
高校では自然数の素因数分解の一意性は学びますが、なぜそうなるかは説明されません。また、ユークリッドの互除法で2つの自然数の最大公約数を求めることができることも知りますが、求まる理由は説明されません。不定一次方程式の解がいつ存在するかも明らかにされないまま、解を求めたりもしています。2つの自然数の公約数はいつでも最大公約数の約数であることを、素因数分解の一意性を使わずに説明できるでしょうか。大学での学修が進めば、これらのことが一挙に解決するばかりではなく、同じようなことが多項式の世界でも成立することを学ぶことになります。
微分方程式
微分方程式の解の存在定理を学修します。その名の通り、微分方程式の解がある条件の下で存在することを保証する定理ですが、存在性が分かっても解の表現の仕方が分からないのでやや抽象的な学びとなります。抽象的というとなんだか興味が薄れてしまいがちですが、数学を研究するには抽象論を理解することはたいへん重要です。一緒にとことん数学の面白さを探求しましょう。
代数学I
整数論(初等整数論)から出発して、群の理論を学んでいきます。群の公理は簡単なものですが抽象的でとっつきにくいものです。しかし「とっつきにくい」群論を、豊富な実例、すなわち群が応用上あらわれる最も自然な姿である対象群を例にとりながら、自然と身につくよう授業を進めていきます。
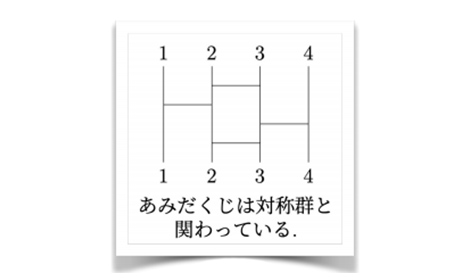
解析学Ⅰ
リーマン積分を用いて具体的な図形の面積や体積を測ることは、高校以来学んできました。本科目では、“測れる”という概念をルベーグの理論により見直すことで、測れる対象を具体的な図形から抽象的な集合へ拡張します。そして、測度と呼ばれる数学的な“測り”を導入することでルベーグ積分を導入します。
RESEARCH
最先端の科学技術を支える多彩な研究ゼミ。
未来の科学技術をリードしていくであろう多彩な分野の研究ゼミを設けています。豊富な経験と実績を有する教授陣による丁寧な指導のもと、学生一人ひとりが最先端の学びに触れ、高度な専門性を身につけたスペシャリストを育てます。専攻の専門領域を超えて幅広く学ぶことが可能です。
研究ゼミピックアップ
「数理解析」
気象予報、コロナウイルスの
流行予測などを微分方程式で解き、
解の性質を調べて現象のメカニズム解明に
つなげていきます。

CHECK 1
「飛行機が飛ぶための気流の解析」「明日の天気を予報する気象予報」など、身の回りで起こる現象を微分方程式を用いてメカニズムを解明。CHECK 2
拡散現象を記述する微分方程式を題材とし、具体的な解析手法を学びます。CHECK 3
少人数のグループで構成し、学生が順番に講師役に。講師役になることで、しっかりと理解し、正確に説明する能力を養成します。
MESSAGE
学生の主体性を重視した学びを取り入れており、積極的な学生は興味の赴くままに多くのことを学ぶことができます!
研究ゼミピックアップ
「空間の幾何学」
高校までの幾何学では、三角形や円のような「紙に描ける図形」を様々な方法で調べますが、本研究ゼミでは、より自由に4次元空間のような「目に見えない空間」の形をも考察の対象とします。大切になるのは、豊かな想像力と感性を言語化する確かな思考力です。大学で学ぶ新たな空間の概念は、近年「データや情報の『形』を調べる」など、数学の抽象性を活かした仕方で応用されています。皆さんの好奇心を刺激する学びを展開します。
研究ゼミピックアップ
「素数の分解性と数の拡大」
どんな整数も素因数分解することができます。素数はそれ以上分解することができない数ですが、数の範囲を拡大すると面白い現象が起きます。例えば素数5は整数の範囲ではこれ以上分解できませんが、虚数単位i(2乗して-1になる数)を導入すると5=(2+i)×(2-i) と2つの数の積に分解することができます。このように、数の範囲を拡大すると素数の性質が失われることがあります。一方で素数3は数の範囲を拡大しても分解することができず、素数の性質を保ちます。本ゼミでは「どのような素数が分解するのか」や「どのような拡大で分解できるか」を研究します。また、通信技術への暗号理論の応用など、実社会にどのように数学的理論が活用されているのかについても考察します。
SPECIALIST
各分野のスペシャリストがあなたを導きます。
研究者の特集記事をご覧ください。
EMPLOYMENT AND QUALIFICATIONS
万全の就職サポート。多彩な資格取得も可能。
少人数教育環境の下、日本を代表する企業との連携を活かして一人ひとりの希望の就職実現を強力サポートするほか、いずれの専攻でも希望者は多彩な資格の取得をめざすことができます。
取得をめざす主な免許・資格
数理科学専攻
- 基本情報技術者
- 応用情報技術者
など
VOICE
先輩VOICE

数学を深く学べて
将来のキャリアにつながる教育。
理工学科 数理科学専攻 4年
大阪府立北千里高等学校出身
数学に興味を持ち、自分の能力を伸ばしたいという思いがあり、数学を深く学べてしかも将来のキャリアにつながる教育を行っている大和大学に進学を決めました。講義では特に、集合と位相の講義が印象に残っています。複雑な概念が絡み合う集合論や位相空間について、教科書では理解出来なかった部分を先生のおかげでクリアに理解できたことが嬉しかったです。教材や説明が抽象的で深遠な内容であったにもかかわらず、分かりやすいアプローチで示していただき、自分の知識が飛躍的に向上しました。先生方の教えが、私にとって数学への興味を一層深めるきっかけとなりました。今後も講義で得た知識を活かし、数学の美しさを追求していきたいと思っています。

大好きな数学を楽しみながら
とことん掘り下げることができます。
理工学科 数理科学専攻 3年
大阪府立登美丘高等学校出身
高校時代からもともと数学が大好きで、大学でさらにもっと深く学んでみたいと考えていました。数理科学専攻は定員30名と少人数な専攻なので先生方との距離も近く、友人もすぐにできる環境です。専門性をどんどん高めていけるだけでなく、他の専攻のことも学べることがとても良いなと思います。今は、将来に活かすため資格・免許の取得に全力を注いでいます。

自分の将来の目標を探し、
実現できる大和大学。
理工学部 数理科学専攻 2年
滋賀県立虎姫高等学校出身
中学生の時に父にTVの特集で放送していたエドワード・フレンケル氏の数学の講義を見せてもらったことが印象に残っています。もともと数学が好きだったことも相まって詳しく数学の勉強をしたいと感じ、数理科学専攻を選びました。大学に入学後、数学そのものの見方が変わったように思います。様々な数学についての本を読んで数々の理論、証明に至るまでにドラマがあって面白いなと感じていますし、また「和算」という新しい分野にも興味をもっています。
自分の将来の目標を探せ、実現できる大和大学で一緒に学びませんか。

5専攻融合型カリキュラムと実践的な授業で日々実力がついていると実感できます。
理工学部 数理科学専攻 4年
大和大学の理工学部では、5専攻融合型カリキュラムで他専攻の講義を受講し、多くの知識に触れることができるので幅広い進路に対応できます。先生方は1年生のうちから就職や大学院進学のことを熱心に考えてくださいます。微積分は高校でも学びましたが、新しい数式や定理が出てきます。数式を解くときに解法がひとつではないことで様々な考え方ができるところが大きな魅力です。その他にも、企業から提示されたミッションの解決策をグループで考えるという講義が将来にとても役立つと感じています。







 アクセス
アクセス 資料請求/問合せ
資料請求/問合せ




 HOME
HOME


















